Note to the reader: please credit the author when using the following equations, graphs, and tables since this is original material.
A NEW DEFINITION OF CAPITALISM: Capitalism is a monetary system which distributes wealth by a definable distribution raised to a power of a base as determined by rank, where the percentage of those with average wealth and above approximately equals the percentage of those with no wealth and debt. Given constant average wealth and median wealth, both values become trivial compared to the wealth of the very richest as the number of entities in the economy increases. Capitalism creates huge levels of wealth inequality by intrinsic exponentiation as determined by rank.
If poverty is considered lack of wealth, then poverty must be intrinsic to capitalism based on empirical evidence from the Survey of Consumer Finances from 1983 to 2007 as compiled and adjusted by Edward N. Wolff in Recent Trends in Household Wealth in the United States: Rising Debt and the Middle-Class Squeeze---an Update to 2007.
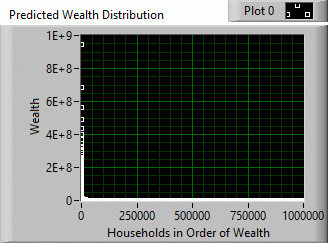
Above is a graph of a hypothetical wealth distribution of an economy of one million households with an average wealth of $369,385 and median wealth of $76,093 using the First General Wealth Equation. The numbers directly above the gray indicators are the actual averaged numbers from the Wolff data from 1983 to 2007. The gray indicators show the computer calculated percentages.
Since the wealth distribution was apparently so skewed, I worked with the natural log of wealth while trying known distributions to describe the data. There were relatively few data points so it was quite a task to either find or create a distribution to fit the data. Eventually I realized the best fit (among commonly used distributions) would be back to back tails of normal distributions as shown in the Natural log of Wealth graph as pictured below:
Entire distribution above is raised as a power to base e to yield the Predicted Wealth Distribution
In order to create a general wealth equation, I believed the equation needed to be scalable in both the wealth and population axes. I found the trick to doing this is taking the famous "Bell Curve" Normal Distribution Probability Distribution Function and modifying it where frequency (people) and probability (wealth) switch axes, where only positive values of wealth are allowed, and where the mean and standard deviation become zero and one respectively to create my First General Wealth Equation:
Wi is an individual's wealth, Ri is the individual's rank either above or below the top 20% in equal decrements in descending order, and A and M are an offset and multiplier respectively.
To evaluate from the top 20% to the wealthiest, use the equation in this form:
To evaluate from the top 20% to the bottom 17.6375%, use the equation in this form:
(Note: You can view every article as one long page if you sign up as an Advocate Member, or higher).