Introduction
The concept of four-dimensional spacetime pre-dates relativity theory, but with relativity there is a revolutionary understanding of the covariance of space and time. The prevailing understanding of the relativistic, covariant, spacetime continuum is due primarily to H. Minkowski's geometrical contribution (1908) to Einstein's Special Theory. Minkowski saw in the relativistic interpretation of the Lorentz transformations1 the possibility for a two-dimensional representation of the peculiar interrelationships between bodies having large relative velocities. Assuming the validity of the tenets of Relativity, and assuming the correctness of the geometric representation, it was expected that the graphic would express and corroborate relativity in its mathematical form, that "physical laws might find their most perfect expression" (Minkowski, 1908, 76), and facilitate further insights into the nature of what Minkowski called the spacetime continuum.
Diagramming spacetime
Figure 1 is a typical Minkowski diagram, with the vertical or nearly vertical axes of two reference frames representing time and the horizontal or nearly horizontal axes representing their spatial dimensions. A defining characteristic of the diagram is a diagonal vector or vectors projecting the motion of light relative to the motion of an observer who is moving in time on the vertical axis while "at rest" in space.
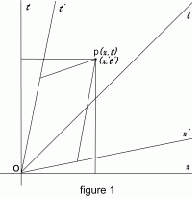
A typical Minkowski diagram. The world-line of the observer is moving in time perpendicular to the space axis. The world-line of a ray of light is depicted as a diagonal in the observerâ??s coordinate system, moving in equal parts of space and time. Point
(Image by James Arnold) Details DMCA
The primary interests in the diagram have generally focused on relative location of events in spacetime, as with point p in figure 1, and on the "light-cones" formed by the relative motion of light-rays. But with attention to world-lines, there can be seen a remarkable, pre-relativistic flaw in the Minkowskian projection: The world-line of a body moving relative to the observer is shown to be moving in space as observed, but moving in time as-if it is moving in synchronicity with the observer's clock, not dilated (slowed) according to theory. In other words, it isn't projected as it should be, compared to the observer's clock, but rather along with the observer's clock.
There is no more important precept in relativity theory than that in describing the relative motion of a body we must specify the frame of reference from which the observation is being made, and we must distinguish the observed body's metrics of space and time from the observer's. If for example it is said that a body is observed to travel 8 light-seconds (ls) in 10 seconds (sec), unless we are to return to the absolutes of classical physics we must specify and distinguish according to whose measures of distance and time. To fully describe the observed motion relativistically is to report that the body travels 8 ls in space relative to an observer's uniform or stationary spatial reference, and a number of sec in time (t') that is relative to the observer's corresponding temporal reference of 10 sec (t), at a relative velocity of v (expressed as .8, proportional to c) 2. The relationship can be expressed by t' = t SQRT(1-v2) per a Lorentz transformation, or alternately by t' = SQRT(t2-x2), with x as the relative distance traveled in space, calibrated in light-seconds, which in the above example yields either 10(SQRT(1-.82)) or SQRT(102-82) = 6. Strictly speaking, therefore, the body under consideration travels a relative 8 ls and 6 sec (its clock is observed to tick 6 seconds), and we measure its travel from a reference frame at 0 ls and 10 sec.
The significance of the distinction between the pre-relativistic and relativistic accounts is most striking in the description of light: When it is said in a Newtonian perspective that light travels (approximately) 300,000 km (1 ls) in 1 sec, we make a relativistic correction and say, as in the above example, it actually travels 10 ls relative to the observer's uniform motion or state of rest in space and 0 sec (t' = 10(SQRT(1-02) or SQRT(102-102)) relative to the observer's duration of 10 sec in time.
To neglect the relativistic correction is to invite a serious error in one's understanding of spacetime, and yet it is an oversight built-in to the Minkowski diagram. The diagonal light-vectors (the "light-cones") in the diagram makes this conclusion unavoidable: To project the world-line of light as moving 10 ls in space and 10 sec in time (a spacetime diagonal, one side of a "light cone" in the Minkowski diagram) is to describe the relative motion of light in space, but in terms of the observer's own reference in time, treated as an independent, absolute measure. This is a critical misrepresentation of a most fundamental precept of relativity theory -- that time is relative and referential.
The Minkowski diagram has prevailed so long, the point cannot be overstressed: It is the clock of the moving body that indicates how it is moving in time, not the clock of the observer. Hence the two-dimensional representation of the world-line of the observed body must express its own clock as measured by the observer, as well as its relative distance traveled.
An alternative diagram (figure 2) conforming to Special Relativity and the Lorentz transformations, and treating both space and time as relative, provides a heuristic representation by means of which, as Minkowski originally envisioned, "physical laws might find their most perfect expression."
The x-axis in figure 2 represents space calibrated in light-seconds, while its perpendicular, the y-axis, represents time calibrated in seconds -- both according to observer A, who is considered to be at rest and moving in time along the y-axis. Vector B represents a body in motion relative to A.
A travels 10 sec in time in the scope of the diagram while "at rest" (i.e., moving perpendicular) to space in time. Body B, which as a matter of convenience is located initially with A at the origin o, moves from the vicinity of A at a velocity, according to A, which takes it 8 ls in 10 sec. The final spacetime coordinates of B according to A (8,6) can be derived from the Lorentz transformations, or geometrically by measurement of the lengths in the diagram. By locating B at 6 seconds in time it is represented that the clock of B has moved 6 sec in the coordinate system of A. (Note that at a velocity of .8c the world-line of B has already transgressed the diagonal of the Minkowskian light-cone.)
The Utility of a relativistic diagram
Next Page 1 | 2 | 3 | 4 | 5 | 6
(Note: You can view every article as one long page if you sign up as an Advocate Member, or higher).






